Answer
given,
thickness of a flange on an aircraft component is uniformly distributed between 0.95 and 1.05 millimeters.
X = U[0.95,1.05] 0.95≤ x ≤ 1.05
the cumulative distribution function of flange
F(x) = P{X≤ x}=
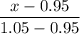
=
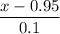
b) P(X>1.02)= 1 - P(X≤1.02)
=
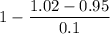
= 0.3
c) The thickness greater than 0.96 exceeded by 90% of the flanges.
d) mean =
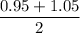
= 1
variance =
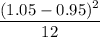
= 0.000833