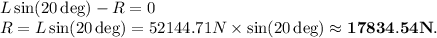Question

The helicopter in the drawing is moving horizontally to the right at a constant velocity. The weight of the helicopter is W=49000 N. The lift force L generated by the rotating blade makes an angle of 21.0° with respect to the vertical. (a) What is the magnitude of the lift force? (b) Determine the magnitude of the air resistance R that opposes the motion.

Answer 1

(a) The magnitude of the lift force is 52144.71 N, approximately.

(b) The magnitude of the air resistance force opposing the movement is 17834.54 N, approximately.

Step-by-step explanation:

Since the helicopter is moving horizontally at a constant velocity, we can assume that the net force acting on it is zero, then

(a) in the vertical direction we have

`L\cos(20\deg)-W=0\\L=(W)/(\cos(20\deg))=(49000 N)/(\cos(20\deg))\approx \mathbf{52144.71 N}`.

(b) Now horizontally,

`L\sin(20\deg)-R=0\\R=L\sin(20\deg)=52144.71 N* \sin(20\deg) \approx \mathbf{17834.54 N}.`