Answer:
Ans.
a) To pay off the debt, it would take 190.26 years at a rate of $2,500/second
b) The quantity of dollar bills attached end to end that would take to reach the Moon is 2,478,116,129
Step-by-step explanation:
Hi, we are going to need to do some adjustments to the speed equation of physics (for a.) and a unit conversion for b.
Let´s see the equation that we need for a.
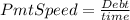
Therefore.
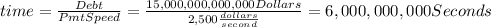
Now, we need to convert this to years, that is:
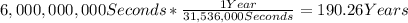
Now, for b) we need to establish the leght of a dollar bill in meters, that is.
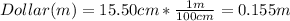
And now, since we know the length of a dollar bill in meters, let´s find out how many would it take to reach the moon.
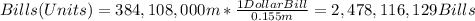
Best of luck.