Question

An electric motor operating at steady state draws a current of 20 amp at a voltage of 110 V. the output shaft rotates at a constant speed of 2000 RPM and exerts a torque of 9.07 N middot m. Determine the input power, in W. the output power, in W. the cost of 24 hours of operation if electricity is valued at $0.09 per kW middot h.

Answer 1

Input power = 2200 w

Output power = 1899.7 w

Cost = $ 4.752

Step-by-step explanation:

Assuming a Direct Current scenario, electric input power is calculated by:

`Pi = V * I`

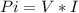
Where

Pi is Power in watts (w)

V is voltage in volts (v)

I is current in amperes (a)

`Pi = V * I = 110 v * 20 a = 2200 w`

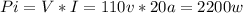
Then, the formula for output power is

`Po = T * S / 9.5488`

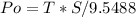
Where

Po is Power in watts (w)

T is torque in NM (v)

S is speed in RPM (rpm)

9.5488 is used to convert rpm unit to rad/sec unit

`Po = T * S / 9.5488 = 9.07 NM * 2000 rpm / 9.5488 = 1899.7 w`

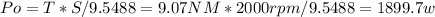
Finally, to calculate the cost of operation, we simply multiply the input power, total hours of operation and value per hour:

`CO = Pi * H * C / 1000`

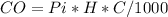
Where

CO is cost of operation in $

Pi is Power in watts (w)

H is operation time in hours (hs)

C is value per kw per hour (kwh)

1000 is used to convert watts unit to kilowatts unit

`C = Pi * H * C / 1000 = 2200 w * 24 hs * 0.09 $ / 1000 = 4.752`$