Answer:
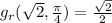
Explanation:
First, notice that:
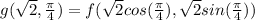
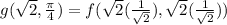
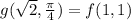
We proceed to use the chain rule to find
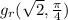 using the fact that
using the fact that
 to find their derivatives:
to find their derivatives:
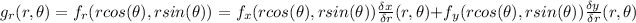
Because we know
 then:
then:
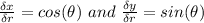
We substitute in what we had:
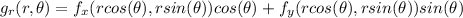
Now we put in the values
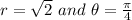 in the formula:
in the formula:
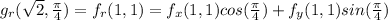
Because of what we supposed:
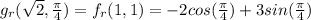
And we operate to discover that:
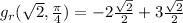
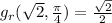
and this will be our answer