On a certain day, a bakery produced a batch of rolls at a total production cost of $300. On that day, (4)/(5) of the rolls in the batch were sold, each at a price that was 50 pe…

Question

On a certain day, a bakery produced a batch of rolls at a total production cost of $300. On that day,
`(4)/(5)` of the rolls in the batch were sold, each at a price that was 50 percent greater than the average (arithmetic mean) production cost per roll. The remaining rolls in the batch were sold the next day, each at a price that was 20 percent less than the price of the day before. What was the bakery's profit on this batch of rolls?

A. $ 150
B. $ 144
C. $ 132
D. $ 108
E. $ 90

Answer 1

The profit of the bakery for this batch of rolls is C. $ 132

Explanation:

You know the following this about the problem:

• xy=300 is the total cost of the production of the rolls, where x is the cost of the rolls and y is the number of rolls.
• Day 1 the bakery sold 4/5 of the rolls at 1.50 its value.
• Day 2 the bakery sold 1/5 of the rolls ar 0.8 of the price of Day 1.

`Day1=1.50x(4)/(5)y=(3)/(2)x(4)/(5)y=(6)/(5)xy\\Day2=0.8(3)/(2)x(1)/(5)y=(4)/(5)(3)/(2)x(1)/(5)y=(6)/(25)xy`

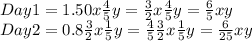
The total gain of the sales is:

Day 1 + Day 2

`Day1+Day2=(6)/(5)xy+(6)/(25)xy=(36)/(25)xy`

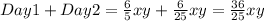
and you know that xy =300, then the total gain is:

`gain=(36)/(25)(300)=432`

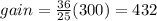
And the profit is the total gain less the total cost:

Profit = 432-300=132