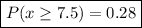Answer:
The probability that the baby will weigh more than 7.5 lbs is
 0.28
0.28
Explanation:
Let's call
 the weights of babies born to full-term pregnancies. As the problems states that this follows roughly a Normal distribution, and that in Meadowbrook Hospital this distribution has a mean value (
the weights of babies born to full-term pregnancies. As the problems states that this follows roughly a Normal distribution, and that in Meadowbrook Hospital this distribution has a mean value (
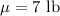 ) with an standard deviation
) with an standard deviation
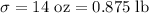 .
.
Thus, for this hospital we can say
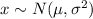 . Note that
. Note that
 is the variance of the distribution and not the standard deviation, which is the square root of the variance. For our problem we have:
is the variance of the distribution and not the standard deviation, which is the square root of the variance. For our problem we have:
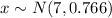 .
.
The probability of an event is then given by:
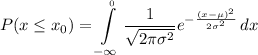
Now the probability that the baby will weigh more than 7.5 lbs is given by:
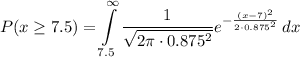
Calculating the integral we obtain: