Answer:
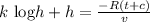 is the solution to the given differential equation.
is the solution to the given differential equation.
Explanation:
We are given the following information in the graph:
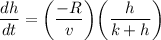
where h is the hormone concentration in the bloodstream, R is the maximum transport rate, t is time, v is the volume of the capillary, and k is a positive constant that measures the affinity between the hormones.
We have to solve the given differential equation:
