Question

A biologist wishes to feed laboratory rabbits a mixture of two types of foods. Type 1 contains 8g of fat, 12g of carbs, and 2g of protein per ounce. Type 2 contains 12g of fat, 12g of carbs, and 1g of protein per ounce. Type 1 costs $0.20 per ounce and Type 2 costs $0.30 per ounce. The rabbits each receive a daily minimum of 24g of fat, 36g of carbs, and 4g of protein, but get no more than 5 oz. of food per day. If each food type must be fed, how many ounces of each food type should be given to satisfy the dietary requirements at a minimum cost? (HINT: There are 4 constraints.)

Answer 1

we have minimize cost by feeding the rabbits 3 ounces of feed 1 and 0 ounces of feed 2.

Step-by-step explanation:

let x be the ounces of feed 1

let y be the ounces of feed 2

according to the information we have following inequalities

Fat grams:
`8x + 12y \geq 24`

Carb grams:
`12x + 12y \geq 36`

`x + y \leq 3`

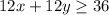
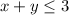
Protein grams:
`2x + y \geq 4`

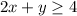
Total food:
`x + y \leq 5`

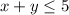
for cost we have

C = 0.20x + 0.30y

Thus, we have the limitation of:

`5 \geq x + y \geq 3`

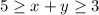
plotting all inequalities we have found pentagon with following points

(0,5)

C = 0.20(0) + 0.30(5) = 1.50

(0,4)

C = 0.20(0) + 0.30(4) = 1.20

(1,2)

C = 0.20(1) + 0.30(2) = 0.80

(3,0)

C = 0.20(3) + 0.30(0) = 0.60

(5,0)

C = 0.20(5) + 0.30(0) = 1.00

Thus, we have minimize cost by feeding the rabbits 3 ounces of feed 1 and 0 ounces of feed 2.