Question

The personnel department of a large corporation wants to estimate the family dental expenses of its employees to determine the feasibility of providing a dental insurance plan. A random sample of 12 employees reveals the following family dental expenses (in dollars): 115 370 250 593 540 225 117 425 318 182 275 228 Construct a 95% confidence interval for the average family dental expenses for all employees in this corporation. Place your LOWER limit, in dollars rounded to 1 decimal place, in the first blank. Do not use a dollar sign, a comma, or any other stray mark. For example, 123.4 would be a legitimate entry. Place your UPPER limit, in dollars rounded to 1 decimal place, in the second blank. Do not use a dollar sign, a comma, or any other stray mark. For example, 567.8 would be a legitimate entry.

Answer 1

The 95% confidence interval for the average family dental expenses for all employees in this corporation is $211.2 to $405.3.

Explanation:

To construct a 95% confidence interval for the average family dental expenses, we use the formula:

`\[ \bar{X} \pm \left( t * (s)/(√(n)) \right) \]`

where
`\(\bar{X}\)` is the sample mean,
`\(s\)` is the sample standard deviation,
`\(n\)` is the sample size, and (t) is the t-value from the t-distribution corresponding to a 95% confidence level with
`\(n-1\)` degrees of freedom.

First, calculate the sample mean
`(\(\bar{X}\))` and sample standard deviation
`(\(s\))`:

`\[ \bar{X} = (\sum_(i=1)^(12) X_i)/(n) \]`

`\[ s = \sqrt{\frac{\sum_(i=1)^(12) (X_i - \bar{X})^2}{n-1}} \]`

Using the given data,
`\(\bar{X} = 297.8\)` and
`\(s = 142.6\)`. The degrees of freedom
`(\(n-1\)) is \(11\).`

Next, find the t-value for a 95% confidence interval with (11) degrees of freedom. Looking up this value, we find
`\(t = 2.201\).`

Now, substitute these values into the formula to find the margin of error:

`\[ \text{Margin of Error} = t * (s)/(√(n)) \]`

`\[ \text{Margin of Error} = 2.201 * (142.6)/(√(12)) \]`

The margin of error is then added and subtracted from the sample mean to find the confidence interval:

`\[ \text{Lower Limit} = \bar{X} - \text{Margin of Error} \]`

`\[ \text{Upper Limit} = \bar{X} + \text{Margin of Error} \]`

Therefore, the 95% confidence interval is
`\(211.2\) to \(405.3\).`

Answer 2

CI(95%): [205,5;400.8]dolars

Explanation:

Hello!

So you need to construct a confidence interval for the average family dental expenses (μ) using the sample given in the problem. To estimate it you need to first choose a statistic. For this small sample, considering that the variable has a normal distribution (I made a quick Shapiro Wilks test, with p-value 0.3234, you can assume normality) the best statistic to use is the Student's t-test.

t= [x(bar)-μ]/S/√n ≈ t₍ₙ₋₁₎

The formula for the confidence interval to estimate the mean is

x(bar)±
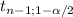`t_(n-1; 1-\alpha/2)`* (S/√n)

The critical value is from a t-distribution with 11 degrees of freedom

±
`t_(n-1; 1-\alpha/2) = t_(11; 0.975) = 2.201`

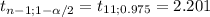
>remember since it's two-tailed, to get the right critical value you have to divide α by 2. So in the text, you received a confidence level of 1-α=0.95 so α=0.05 then α/2=0.025 and 1-α/2=0.975

To construct the interval, you need to first calculate the sample mean and the standard derivation.

Sample

115; 370; 250; 593; 540; 225; 117; 425; 318; 182; 275; 228

n= 12

∑xi = 3638 ∑xi² = 1362670

Sample mean

x(bar): (∑xi)/n = 3638/12 = 303.17 dolars

Standard derivation

S²= 1/n-1*[∑xi²- (∑xi)²/n] = 1/11 * [1362670-((3638)²/12)] = 23614.47 dolars²

S= 153.67 dolars

Confidence interval (95%)

303.17± 2.201* (153.67/√12)

[205,5;400.8]dolars

I hope you have a SUPER day!