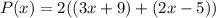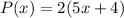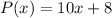Answer:
Part 1)
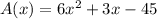
Part 2)
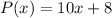
Explanation:
Let
L -----> the length of a rectangular playground
W ---> the width of a rectangular playground
we have
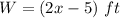
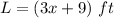
step 1
Find the area of the playground
The area of a rectangle is equal to

substitute the given values
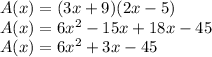
step 2
Find the perimeter of the playground
The perimeter of a rectangle is equal to
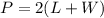
substitute the given values