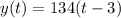Question

A swimmer enters the water and swims in a straight line at 54 meters per minute. Another swimmer enters the water

3 minutes later, swimming in the same direction at 134 meters per minute. Which parametric equations could model

the swimmers' paths from the time the first swimmer entered the water?

Answer 1

A on Edge

Explanation:

Answer 2

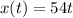`x(t) = 54t` and
`y(t) = 134(t - 3)`

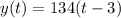
Explanation:

Represent the swimmers with A and B

For Swimmer A:

`Rate = 54m/min`

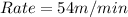
For Swimmer B:

`Rate = 134m/min`

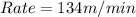
Required:

Write a parametric equation

For Swimmer A:

If swimmer A covers 54 meters in 1 minutes, then the swimmer covers 54t in t minutes

So, the function is:

`x(t) = 54t`

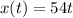
For Swimmer B:

If swimmer A covers t minutes, swimmer B swims for (t - 3) minutes because swimmer B starts 3 minutes later.

If in 1 minutes, swimmer B covers 134 minutes; In (t - 3) minutes, the swimmer covers 134(t - 3)

So, the rate is:

`y(t) = 134(t + 3)`

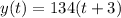
Hence, the parametric functions are:

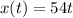`x(t) = 54t` and

`y(t) = 134(t - 3)`