Question

Ackerman and Goldsmith (2011) report that students who study from a screen (phone, tablet, or computer) tended to have lower quiz scores than students who studied the same material from printed pages. To test this finding, a professor identifies a sample of n 5 16 students who used the electronic version of the course textbook and determines that this sample had an average score of M 5 72.5 on the final exam. During the previous three years, the final exam scores for the general population of students taking the course averaged m 5 77 with a standard deviation of s 5 8 and formed a roughly normal distribution. The professor would like to use the sample to determine whether students studying from an electronic screen had exam scores that are significantly different from those for the general population.

Answer 1

The scores are significantly lower than those from the general population.

Explanation:

Hello!

To make the test we need to first identify the hypothesis we want to test. In this case, the hypothesis statement is

"Studying from a screen lowers the scores on the final exam"

Should this happen, it would mean that the average scores on the final exam will be lowered too. If this statement is not true, the average scores on the final exam should not change whether the students use virtual or printed materials to study.

On the other hand, we will take the previously known information as population reference, so for this example, the population mean is 577 and the standard deviation 58

With this in mind, we can state the null and alternative hypothesis:

H₀: μ = 577

H₁: μ < 577

The text doesn't specify a significance level, so I'll use the most common one. α=0.05

For this text, since we have a large sample (n=516), the variable has a normal distribution and its parameters known, we'll use a Z-test.

Z= (x(bar)-μ)/(σ/√n) ≈ N(0;1)

Critical region.

The rejection region is one-tailed, this is depicted in the hypothesis since it says the scores "lower" when virtual materials are used to study. So we will reject the null hypothesis if the calculated Z-value is less than the critical value.

Our critical value bein a
`Z_(\alpha )` =
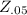`Z_(\0.05)` = -1.64

So we will reject the null hypothesis if the
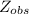`Z_(obs)` is ≤-1.64 or support the null hypothesis if the
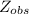`Z_(obs)`is >-1.64

Next we calculate the Z-value

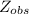`Z_(obs)`= (x(bar)-μ)/(σ/√n) = (572.5-577)/(58/√516)= -4.5/2.55 = -1.76

since
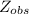`Z_(obs)`= -1.76 ≤ -1.64 we will reject the null hypothesis.

In other words, we can assume that the average scores on the final exam decrease when the students use virtual materials to study.

I hope you have a SUPER day!