Question

Allison and Leslie, who are twins, just received $15,000 each for their 26th birthday. They both have aspirations to become millionaires. Each plans to make a $5,000 annual contribution to her "early retirement fund" on her birthday, beginning a year from today. Allison opened an account with the Safety First Bond Fund, a mutual fund that invests in high-quality bonds whose investors have earned 6% per year in the past. Leslie invested in the New Issue Bio-Tech Fund, which invests in small, newly issued bio-tech stocks and whose investors have earned an average of 17% per year in the fund's relatively short history. If the two women’s funds earn the same returns in the future as in the past, how old will each be when she becomes a millionaire? Do not round intermediate calculations. Round your answers to two decimal places.

Answer 1

Allison: age 67

Leslie: 46 years

Step-by-step explanation:

We are asked to find at which time the fund equal 1,000,000

both sister fund compose of a 15,000 lump sum and ordinary annuity of 5,000 dollars the difference will be the rate at which each capital works:

Alison:

`15,000* (1.06)^(n) + 5,000 (1.06^(n)-1)/(0.06) = 1,000,000\\`

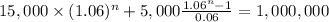
We divide by 5,000

`3* (1.06)^(n) + (1.06^(n)-1)/(0.06) = 200\\`

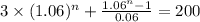
Then we clear the part:

`1.06^(n) = (200 - 3 (1.06)^(n))*0.06 +1 \\`

`1.06^(n) = 13 - 0.18(1.06)^(n)`

`1.18 (1.06)^(n) = 13`

`(1.06)^(n) = 13/1.18`

`(1.06)^(n) = 11.0169491`

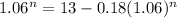
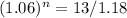
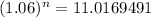
we use logarithmic properties to solve for n:

`log 11.0169491 / log 1.06`

41.17864898

Allison will be a millionaire after 41.17 year. She start at age 26 so at age 67 she achieve his goal.

Leslie:

`15,000* (1.17)^(n) + 5,000 (1.17^(n)-1)/(0.17) = 1,000,000\\`

`3* (1.17)^(n) + (1.17^(n)-1)/(0.17) = 200\\`

`1.17^(n) = (200 - 3 (1.17)^(n))*0.17 +1 \\`

`1.17^(n) = 35 - 0.51(1.17)^(n)`

`1.17^(n) = 35/1.51`

`log 23.178807947 / log 1.17`

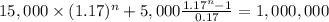
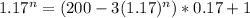
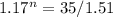
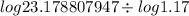
n = 20.02014878

Leslie will achieve it in 20.20 years

thus, at age 46