Question

A car of mass 1000.0 kg is traveling along a level road at 100.0 km/h when its brakes are applied. Calculate the stopping distance if the coefficient of kinetic friction of the tires is 0.500. Neglect air resistance. (Hint: since the distance traveled is of interest rather than the time, x is the desired independent variable and not t. Use the Chain Rule to change the variable:
`(dv)/(dt) = (dv)/(dx) (dx)/(dt) = v(dv)/(dx)`.)

Answer 1

Step-by-step explanation:

It is given that,

Mass of the car, m = 1000 kg

Speed of the car, v = 100 km/h = 27.77 m/s

The coefficient of kinetic friction of the tires,
`\mu_k=0.5`

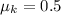
Let f is the net force acting on the body due to frictional force, such that,

`-f=ma`

`a=(-f)/(m)`

`a=(-\mu _k mg)/(m)`

`a=\mu_k g`

`a=-0.5* 9.8`

`a=-4.9\ m/s^2`

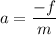
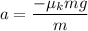
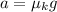
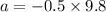
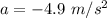
We know that the acceleration of the car in calculus is given by :

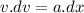`v.dv=a.dx`, x is the stopping distance

`\int\limits^0_v {v.dv}=\int\limits^x_0 {a.dx}`

`(v^2)/(2)|_v^0=ax`

`0-(27.77)^2=-2* 4.9x`

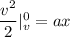
On solving the above equation, we get, x = 78.69 meters

So, the stopping distance for the car is 78.69 meters. Hence, this is the required solution.