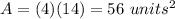Question

The point (2,7) is successively reflected across the x-axis then the y-axis and then the x-axis again. What is the area of the rectangle formed by these two pointer

Answer 1

The area of rectangle is
`56\ units^2`

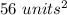
Explanation:

Let

A(2,7)

step 1

The point A is reflected across the x-axis

we know that

The rule of the reflection of a point across the x-axis is

(x,y) -----> (x,-y)

so

A(2,7) ----->B(2,-7)

step 2

The point B is reflected across the y-axis

we know that

The rule of the reflection of a point across the y-axis is

(x,y) -----> (-x,y)

B(2,-7) ----> C(-2,-7)

step 3

The point C is reflected across the x-axis

we know that

The rule of the reflection of a point across the x-axis is

(x,y) -----> (x,-y)

so

C(-2,-7) ----->D(-2,7)

step 4

Find the area of rectangle formed by

A(2,7),B(2,-7),C(-2,-7),D(-2,7)

using a graphing tool

see the attached figure

The area of rectangle is

`A=(4)(14)=56\ units^2`