Answer:
The probability that maximum safe load will be exceeded is 3.9%
Explanation:
We are given the following information in the question:
Mean, μ = 190 pounds
Standard Deviation, σ = 40 pounds
We are given that 50 skiers are randomly chosen from this normally distributed population, hence, by central limit theorem:
Mean, μ = 190 pounds
Standard Deviation,
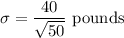
Formula:
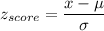
a) P(maximum safe load exceeded)
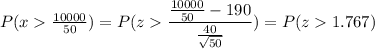
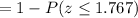
Calculation the value from standard normal z table, we have,
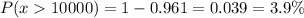
Hence, the probability that maximum safe load will be exceeded is 3.9%