Question

The random variable X, representing the number of items sold in a week, has the following probability distribution: x 0 1 2 3 4 5 6 P(X = x) 0.10 0.20 0.40 0.15 0.05 0.05 0.05 By the fourth day of a particular week, 3 items have already sold. What is the probability that there will be less than a total of 5 items sold during that week?

Answer 1

0.667

Explanation:

Data provided:

x 0 1 2 3 4 5 6

P(X = x) 0.10 0.20 0.40 0.15 0.05 0.05 0.05

Now,

The probability that less than 5 items will be sold in a week given that 3 items have already been sold can be calculated as;

P ( less than 5 items sold | 3 or more items sold )

=
`\frac{\textup{ 3 or more and less than 5 items sold}}{\textup{3 or more items sold}}`

=
`\frac{\textup{3 or 4 items sold}}{\textup{3 or more items sold}}`

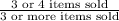
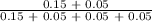
or

P ( less than 5 items sold | 3 or more items sold ) =
`\frac{\textup{0.15 + 0.05}}{\textup{0.15 + 0.05 + 0.05 + 0.05}}`

or

P ( less than 5 items sold | 3 or more items sold ) =
`\frac{\textup{0.2}}{\textup{0.3}}`

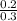
or

P ( less than 5 items sold | 3 or more items sold ) = 0.667