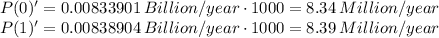Question

The population, P(t), of China, in billions, can be approximated by1 P(t)=1.394(1.006)t, where t is the number of years since the start of 2014. According to this model, how fast was the population growing at the start of 2014 and at the start of 2015? Give your answers in millions of people per year rounded to 2 decimal places. At the start of 2014, the population was growing at million people per year. At the start of 2015, the population was growing at million people per year.

Answer 1

At the start of 2014, the population was growing at 8.34 million people per year.

At the start of 2015, the population was growing at 8.39 million people per year.

Explanation:

To find how fast was the population growing at the start of 2014 and at the start of 2015 we need to take the derivative of the function with respect to t.

The derivative shows by how much the function (the population, in this case) is changing when the variable you're deriving with respect to (time) increases one unit (one year).

We know that the population, P(t), of China, in billions, can be approximated by
`P(t)=1.394(1.006)^t`

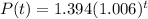
To find the derivative you need to:

`(d)/(dt)\left(1.394\cdot \:1.006^t\right)=\\\\\mathrm{Take\:the\:constant\:out}:\quad \left(a\cdot f\right)'=a\cdot f\:'\\\\1.394(d)/(dt)\left(1.006^t\right)\\\\\mathrm{Apply\:the\:derivative\:exponent\:rule}:\quad (d)/(dx)\left(a^x\right)=a^x\ln \left(a\right)\\\\1.394\cdot \:1.006^t\ln \left(1.006\right)\\\\(d)/(dt)\left(1.394\cdot \:1.006^t\right)=(1.394\cdot \ln \left(1.006\right))\cdot 1.006^t`

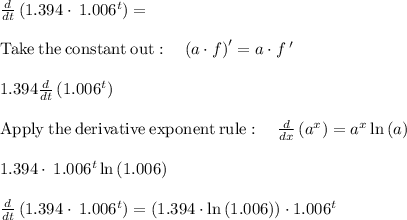
To find the population growing at the start of 2014 we say t = 0

`P(t)' = (1.394\cdot \ln \left(1.006\right))\cdot 1.006^t\\P(0)' = (1.394\cdot \ln \left(1.006\right))\cdot 1.006^0\\P(0)' = 0.00833901 \:Billion/year`

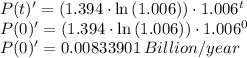
To find the population growing at the start of 2015 we say t = 1

`P(t)' = (1.394\cdot \ln \left(1.006\right))\cdot 1.006^t\\P(1)' = (1.394\cdot \ln \left(1.006\right))\cdot 1.006^1\\P(1)' = 0.00838904 \:Billion/year`

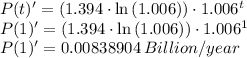
To convert billion to million you multiple by 1000

`P(0)' = 0.00833901 \:Billion/year \cdot 1000 = 8.34 \:Million/year \\P(1)' = 0.00838904 \:Billion/year \cdot 1000 = 8.39 \:Million/year`