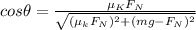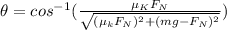Answer:
Step-by-step explanation:
Given
rope makes an angle of

Mass of sled and snow is m
Normal Force
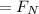
applied Force is F
as Force is pulling in nature therefore normal reaction is given by
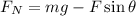
Also
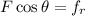
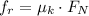

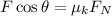 -------1
-------1
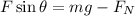 ---------2
---------2
Squaring 1 & 2 and then adding
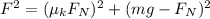
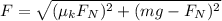
Substitute value of F in 1