Question

You are designing an amusement park ride. A cart with two riders moves horizontally with speed v = 5.40 m/s . You assume that the total mass of cart plus riders is 300 kg. The cart hits a light spring that is attached to a wall, momentarily comes to rest as the spring is compressed, and then regains speed as it moves back in the opposite direction. For the ride to be thrilling but safe, the maximum acceleration of the cart during this motion should be 3.00g. Ignore friction. what is

(a) the required force constant of the bring
(b) the maximun distance the spring will be compressed.

Answer 1

Spring constant required=8910 N/m. Maximum distance compressed=0.99m

Step-by-step explanation:

The first step here is to consider the Newton's Second Law which states that a force F applied to a body of mass m produces an acceleration a. Our body has a mass of 300 kg and the maximum allowable acceleration is 3.00 g. Considering gravity g=9.81m/s^2, a=3.00*9.81m/s^=29.43m/s^2. Hence,

F=300kg*29.43 m/s^2=8829 N

The force that a spring gives is the multiplication of its force constant K and the distance compressed X. . So the force F sholud be equal to K*
`X_(max)`.

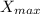F=K*
`X_(max)`.

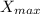Then, when the spring is fully compressed all the kinetic energy of the cart (T) is transferred to the spring as potential elastic energy (U).

`1/2*m*v^2=1/2*K*X_(max)^2` Eq.1

We do not know
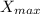`X_(max)` but we do know that it is equal to F/K. Thus,

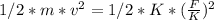`1/2*m*v^2=1/2*K*((F)/(K) )^(2)` Eq.2

Operating in Eq.2
`K=((F)/(v) )^(2) (1)/(m)=8910.75 N/m`

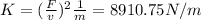
Finally, putting the valus of K in Eq.1 and solving,
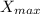`X_(max)`=0.99m