Question

A motorboat heads due east at 16 m/s across a river that flows due south at 9.0 m/s. a.) What is the resultant velocity of the boat? b.) If the river is 136 m wide, how long does it take the motorboat to reach the other side? c.) How far downstream is the boat when it reached the other side of the river?

Answer 1

a)V=18.35 m/s (South -East)

b) t =7.41 m/s

c)D= 66.70 m

Step-by-step explanation:

Given that

Velocity of boat in east direction = 16 m/s

Velocity of river = 9 m/s

a)The resultant velocity V

`V=√(16^2+9^2)\ m/s`

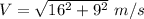
V=18.35 m/s (South -East)

b)

We know that

Distance = Velocity x time

Lets t time takes to cross the river

136 = 18.35 x t

t =7.41 m/s

c)

The distance covered downstream

We know that

Distance = Velocity x time

t= 7.41 s

D= 7.41 x 9 m

D= 66.70 m