Answer:
The mean of x is close to 14.8.
The standard deviation of x is close to 3.78.
Explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and each trial can only have two outcomes, with probabilities
 and
and
 .
.
For an experiment with n repeated trials and a probability of success
 , we have that:
, we have that:
The mean is:

The standard deviation is:

In this problem
There are 400 employees, each with a probability of 3.7% of having food allergy. So
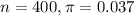 . So:
. So:
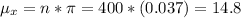
The mean of x is close to 14.8.

The standard deviation of x is close to 3.78.