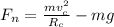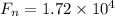Question

The roller coaster car has a mass of 700 kg, including its passenger. If it is released from rest at the top of the hill A, determine the minimum height h of the hill crest so that the car travels around both inside the loops without leaving the track. Neglect friction, the mass of the wheels, and the size of the car. What is the normal reaction on the car when the car is at B and when it is at C? Take ???????? = 7.5 m and ???????? = 5 m.

Answer 1

`h = 18.75 m`

Now when it will reach at point B then its normal force is just equal to ZERO

`N_B = 0`

`F_n = 1.72 * 10^4`

Step-by-step explanation:

Since we need to cross both the loops so least speed at the bottom must be

`v = √(5 R g)`

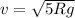
also by energy conservation this is gained by initial potential energy

`mgh = (1)/(2)mv^2`

`v = √(2gh)`

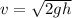
so we will have

`√(2gh) = √(5Rg)`

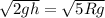
now we have

`h = (5R)/(2)`

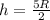
here we have

R = 7.5 m

so we have

`h = (5(7.5))/(2)`

`h = 18.75 m`

Now when it will reach at point B then its normal force is just equal to ZERO

`N_B = 0`

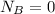
now when it reach point C then the speed will be

`v_c^2 = 2g(h - 2R_c)`

`v_c = 13.1 m/s`

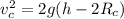
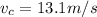
now normal force at point C is given as

`F_n = (mv_c^2)/(R_c) - mg`

`F_n = (700* 13.1^2)/(5) - (700 * 9.8)`

`F_n = 1.72 * 10^4`