Answer: 86.64%
Explanation:
Let x be a random variable that represents the diameter of metal samples.
Given : Population mean :

Standard deviation:
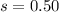
Specified tolerance on the diameter is 0.75 mm.
i.e. range of diameter = 10-0.75< x <10+0.75 = 9.25< x< 10.75
Formula to find the z-score corresponds to x:

At x= 0.75,
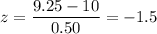
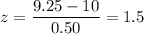
Using standard normal table for z-value,
P-value :
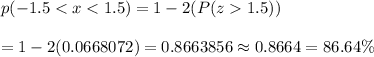
∴ Percentage of samples manufactured using this process satisfy the tolerance specification = 86.64%