Answer: 0.2962
Explanation:
Given : The proportion of all trucks undergoing a brake inspection at a certain inspection facility pass the inspection = 0.75
Since , the proportion of trucks pass the inspection is certain for each ruck.
⇒ It is Binomial distributed.
i.e.
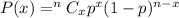
We consider : Groups of 15 trucks and Let X be the number of trucks in a group that have passed the inspection.
i.e. n= 15
Then ,

 [Rounded to nearest 4 decimal places.]
[Rounded to nearest 4 decimal places.]
Hence, the probability that there will be between 8 and 10 trucks (inclusive) which pass the inspection =0.2962