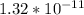Answer:
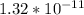
Step-by-step explanation:
Magnetic field
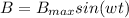
But
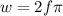 and f is given as 69.5Hz
and f is given as 69.5Hz
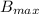 is 0.00100T
is 0.00100T
Flux through cell,
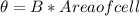
Area of cell=
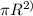 and radius of cell is 6.2µm/2=3.1µm converted to mm it's
and radius of cell is 6.2µm/2=3.1µm converted to mm it's
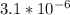
Change in magnetic flux=
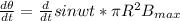
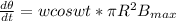
magnitude of induced emf
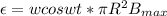 where
where
 gives maximum value of induced emf
gives maximum value of induced emf
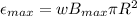
Since
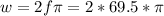 ,
,
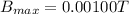 and R=
and R=
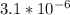
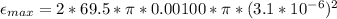
=
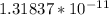
Rounded off to 2 decimal places, max emf=