Question

Although the evidence is weak, there has been concern in recent years over possible health effects from the magnetic fields generated by transmission lines. A typical high-voltage transmission line is 20 m off the ground and carries a current of 200 A . Part A Estimate the magnetic field strength on the ground underneath such a line. Express your answer in microtesla. B B = nothing μT SubmitRequest Answer Part B What percentage of the earth’s magnetic field does this represent? (Assume that magnetic field strength at the surface of the earth is 5× 10 −5 T ) Express your answer in percent. B tl B Earth B t l B E a r t h = nothing % SubmitRequest Answer Provide Feedback Next

Answer 1

A)
`2.0\cdot 10^(-6) T`

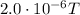
The magnetic field strength around a current-carrying wire is given by the formula

`B=(\mu_0 I)/(2\pi r)`

where

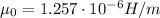`\mu_0 = 1.257 \cdot 10^(-6) H/m` is the vacuum permeability

I is the current in the wire

r is the radial distance from the wire

In this problem, we have

I = 200 A is the current in the wire

and we want to calculate the magnetic field strength at a distance of

r = 20 m

from the wire, so:

`B=((1.257\cdot 10^(-6))(200))/(2\pi (20))=2.0\cdot 10^(-6) T`

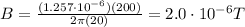
B) 4 %

The magnetic field strength at the surface of the Earth is

`B_e = 5\cdot 10^(-5) T`

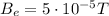
While the strength of the magnetic field generated by the wire at ground level is

`B=2.0\cdot 10^(-6) T`

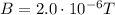
Therefore, in percentage, it is:

`(B)/(B_e)=(2.0\cdot 10^(-6))/(5\cdot 10^(-5))\cdot 100 = 0.04 \cdot 100 = 4 \%`