Answer:
The correct answer is 30,97 ft/s.
Step-by-step explanation:
I looked for the problem and found the situation in which to calculate the speed of the brick.
"Someone edges the brick off the roof, and it begins to fall. What is the brick’s kinetic energy when it is 35 ft above street level?"
Initially, the kinetic energy is zero and the potential energy is equal to 610 J. As the energy is conserved, we must calculate the speed of the brick when it is 35 ft above street level.
First we calculate the mass of the brick at the starting point.
E = m * g * h
610 J = m * 32.16
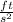 * 50 ft
* 50 ft
m =
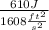
m = 0,38
Now we must calculate the speed when the brick is 35 ft above street level.
E = 610 J
E =
 * m *
* m *
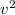 + m * g * h
+ m * g * h
610 J =
 * 0.38 *
* 0.38 *
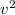 + 0.38 * 32.16
+ 0.38 * 32.16
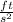 * 35 ft
* 35 ft
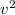 =
=
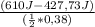
v =
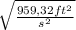
v = 30.97 ft/s
The speed of the brick when it falls and is 35 ft above street level is 30.97 ft/s.
Have a nice day!