Question

An important factor in solid missile fuel is the particle size distribution. Significant problems occur if the particle sizes are too large. From production data in the past, it has been determined that the particle size (in micrometers) distribution is characterized by f(x) = 3x −4, x>1, 0, elsewhere. (a) Verify that this is a valid density function. (b) Evaluate F(x). (c) What is the probability that a random particle from the manufactured fuel exceeds 4 micrometers?

Answer 1

(a) f(x) is a valid density function.

(b)
`F(x)=\left \{ {1-x^(-3)}\qquad {\:x \:> \:1} \atop {0}\quad\qquad{elsewhere} \right`

(c) The probability that a random particle from the manufactured fuel exceeds 4 micrometers is
`P(X>4)=0.0156`.

Explanation:

We know the particle size (in micrometers) distribution is characterized by

`f(x)=\left \{ {{3x^(-4)}\quad {if \:x \:> \:1} \atop {0}\quad{\:elsewhere} \right.`

(a) For f(x) to be a legitimate probability density function, it must satisfy the following two conditions:

1. 
   `f(x)\geq 0` for all x
2. 
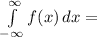   `\int\limits^(\infty)_(-\infty) {f(x)} \, dx =` area under the entire graph of f(x) = 1

It holds that
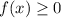`f(x)\geq 0` for all
`x \in \mathbb{R}` and

`\int\limits^(\infty)_(-\infty) {f(x)} \, dx = \int\limits^(\infty)_(-\infty) {3x^(-4)} \, dx=\int\limits^(\infty)_(1) {3x^(-4)} \, dx \\\\\int\limits^(\infty)_(1) {3x^(-4)} \, dx = [-x^(-3)]_(\infty)^(1)} \right = 0-(-1)=1`

Therefore f(x) is a valid density function.

(b) The cumulative distribution function (CDF) F(x) for a continuous rv X is defined for every number x by

`F(x)= P(X\leq x)=\int\limits^x_(-\infty) {f(y)} \, dy`

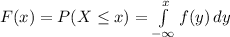
Applying the CDF definition we get:

For
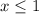`x\leq 1` F(x) = 0, while for
`x>1`

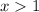
`\int\limits^x_(-\infty) {f(y)} \, dy=\int\limits^x_(-\infty) {3y^(-4)} \, dy=\int\limits^x_(1) {3y^(-4)} \, dy\\\\\int\limits^x_(1) {3y^(-4)} \, dy=[-y^(-3)]_(1)^(x)} \right=1-x^(-3)`

Because f(x) is a piece-wise function, we have

`F(x)=\left \{ {1-x^(-3)}\qquad {\:x \:> \:1} \atop {0}\quad\qquad{elsewhere} \right`

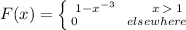
(c) To find the probability that a random particle from the manufactured fuel exceeds 4 micrometers, you need to use the CDF,

`P(X>4)=1-P(X\leq 4)=1-F(4)=1-(1-4^(-3))=4^(-3)=0.0156`