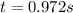Answers:
a)
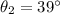
b)
Step-by-step explanation:
This situation is a good example of the projectile motion or parabolic motion, in which the travel of the snowball has two components: x-component and y-component. Being their main equations as follows for both snowballs:
Snowball 1:
x-component:
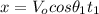 (1)
(1)
Where:
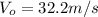 is the initial speed of snowball 1 (and snowball 2, as well)
is the initial speed of snowball 1 (and snowball 2, as well)
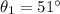 is the angle for snowball 1
is the angle for snowball 1
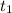 is the time since the snowball 1 is thrown until it hits the opponent
is the time since the snowball 1 is thrown until it hits the opponent
y-component:
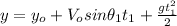 (2)
(2)
Where:
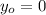 is the initial height of the snowball 1 (assuming that both people are only on the x axis of the frame of reference, therefore the value of the position in the y-component is zero.)
is the initial height of the snowball 1 (assuming that both people are only on the x axis of the frame of reference, therefore the value of the position in the y-component is zero.)
 is the final height of the snowball 1
is the final height of the snowball 1
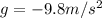 is the acceleration due gravity (always directed downwards)
is the acceleration due gravity (always directed downwards)
Snowball 2:
x-component:
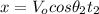 (3)
(3)
Where:
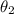 is the angle for snowball 2
is the angle for snowball 2
 is the time since the snowball 2 is thrown until it hits the opponent
is the time since the snowball 2 is thrown until it hits the opponent
y-component:
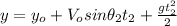 (4)
(4)
Having this clear, let's begin with the answers:
a) Angle for snowball 2
Firstly, we have to isolate
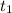 from (2):
from (2):
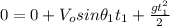 (5)
(5)
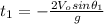 (6)
(6)
Substituting (6) in (1):
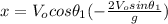 (7)
(7)
Rewritting (7) and knowing
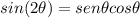 :
:
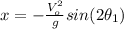 (8)
(8)
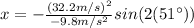 (9)
(9)
 (10) This is the point at which snowball 1 hits and snowball 2 should hit, too.
(10) This is the point at which snowball 1 hits and snowball 2 should hit, too.
With this in mind, we have to isolate
 from (4) and substitute it on (3):
from (4) and substitute it on (3):
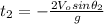 (11)
(11)
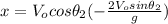 (12)
(12)
Rewritting (12):
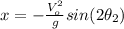 (13)
(13)
Finding
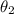 :
:
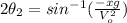 (14)
(14)
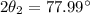
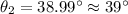 (15) This is the second angle at which snowball 2 must be thrown. Note this angle is lower than the first angle
(15) This is the second angle at which snowball 2 must be thrown. Note this angle is lower than the first angle
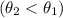 .
.
b) Time difference between both snowballs
Now we will find the value of
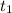 and
and
 from (6) and (11), respectively:
from (6) and (11), respectively:
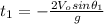
 (16)
(16)
 (17)
(17)
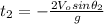
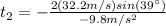 (18)
(18)
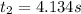 (19)
(19)
Since snowball 1 was thrown before snowball 2, we have:
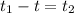 (20)
(20)
Finding the time difference
 between both:
between both:
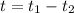 (21)
(21)
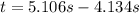
Finally: