Question

The mass percent of Cl⁻ in a seawater sample is determined by titrating 25.00 mL of seawater with AgNO₃ solution, causing a precipitation reaction. An indicator is used to detect the end point, which occurs when free Ag⁺ ion is present in solution after all the Cl⁻ has reacted. If 63.30 mL of 0.2850 M AgNO₃ is required to reach the end point, what is the mass percent of Cl⁻ in the seawater (d of seawater = 1.024 g/mL)?

Answer 1

2.5 %

Step-by-step explanation:

Considering:

`Molarity=(Moles\ of\ solute)/(Volume\ of\ the\ solution)`

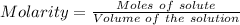
Or,

`Moles =Molarity * {Volume\ of\ the\ solution}`

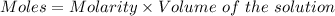
Given :

For
`AgNO_3` :

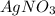Molarity = 0.2850 M

Volume = 63.30 mL

The conversion of mL to L is shown below:

1 mL = 10⁻³ L

Thus, volume = 63.30 × 10⁻³ L

Thus, moles of
`AgNO_3` :

`Moles=0.2850 * {63.30* 10^(-3)}\ moles`

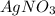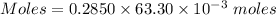
Moles of
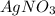`AgNO_3` = 0.0180405 moles

Moles of
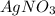`AgNO_3` = Moles of
`Cl^-`

Thus, Moles of
`Cl^-` = 0.0180405 moles

Molar mass of
`Cl^-` = 35.453 g/mol

Mass = Moles * Molar mass = 0.0180405 moles * 35.453 g/mol = 0.6396 g

Volume of sea water = 25.00 mL

Density = 1.024 g/mL

Density = Mass / Volume

Mass = Density * Volume = 1.024 g/mL * 25.00 mL = 25.6 g

`Mass\ \%=(Mass_(Chloride ion))/(Total\ mass)* 100`

`Mass\ \%=(0.6396)/(25.6)* 100`

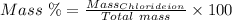
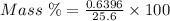
Mass percent of Cl⁻ = 2.5 %