Question

During a circus act, one performer swings upside down hanging from a trapeze holding another, also upside-down, performer by the legs. If the upward force on the lower performer is three times her weight, how much do the bones (the femurs) in her upper legs stretch? You may assume each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius. Her mass is 60.0 kg.

Answer 1

`1.9*10^(-5)m`

Step-by-step explanation:

The elongation in bones is calculated from Euler’s equation of

ΔL=
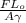`(FL_(o))/(A \gamma )` where F is force, A is cross section area, ΔL is elongation of length,
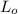`L_(o)` is initial length

To find cross sectional area of the bone,
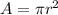`A=\pi r^(2)` and the radius of the leg is given as 0.018m

`A= \pi * (0.0180)^(2)=1.018*10^(-3)`

Since the upward force on lower performer is 3 times her weight,

Total force,
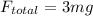`F_(total)= 3mg` where m is mass of performer provided as 60.0kg

`F_(total)= 3*60*9.8= 1764 N`

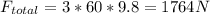
The above force is balanced by two legs hence for each leg,

`F_(leg)= \frac {F_(total)}{2}= \frac {1764}{2}=882N`

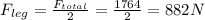
From the formula for elongation initially provided as

ΔL=
`(F_(leg)L_(o))/(A \gamma )`

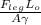
Substituting
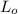`L_(o)` as 0.350m,
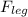`F_(leg)` as 882N
`\gamma = 16*10^(9)`

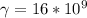
ΔL=
`(F_(leg)L_(o))/(A \gamma )`

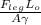
ΔL=
`\ frac {882N * 0.35}{16*10^(9)*1.018*10^(-3)=1.90*10^(-5)m`

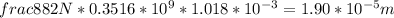
Therefore, elongation is
`1.9*10^(-5)m`