For the given problem, the amount of work done expressed in ergs is 3200 ergs.
Answer: Option A
Explanation:
The work done on an objects are the force acting on it to move the object to a particular distance. So, work done on the object will be directly proportional to the force acting on it and the displacement.
Here, the force acting on the object is given as 0.010 N and the displacement of the object is 0.032 m. So, the work done on the object is
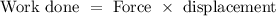
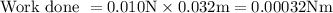
It is known that
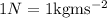
So, the work done can be expressed in
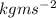 as,
as,
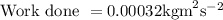
It is known that
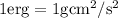 , so the conversion of units from Nm to erg will be done as follows:
, so the conversion of units from Nm to erg will be done as follows:
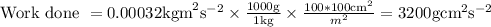
Thus, work done in ergs is 3200 ergs.