Answer:
The tension in the rope is 41.38 N.
Step-by-step explanation:
Given that,
Mass of bucket of water = 14.0 kg
Diameter of cylinder = 0.260 m
Mass of cylinder = 12.1 kg
Distance = 10.7 m
Suppose we need to find that,
What is the tension in the rope while the bucket is falling
We need to calculate the acceleration
Using relation of torque
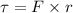
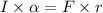
Where, I = moment of inertia
 = angular acceleration
= angular acceleration
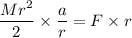
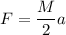 ...(I)
...(I)
Here, F = tension
The force is
 ...(II)
...(II)
Where, F = tension
a = acceleration
From equation (I) and (II)
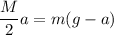
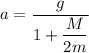
Put the value into the formula
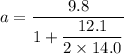

We need to calculate the tension in the rope
Using equation (I)
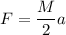
Put the value into the formula

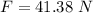
Hence, The tension in the rope is 41.38 N.