Question

Which properties are present in a table that represents an exponential function in the form y-b* when b > 1?

. As the x-values increase, the y-values increase.
II. The point (1, 0) exists in the table.
III. As the x-values increase, the y-values decrease.
IV. As the x-values decrease, the y-values decrease, approaching a singular value.

Answer 1

Answer:I and IV

Explanation:

Answer 2

Properties that are present are

Property I

Property IV

Explanation:

The function given is
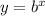`y=b^x` where b > 1

Let's take a function, for example,
`y=2^x`

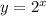
Let's check the conditions:

I. As the x-values increase, the y-values increase.

Let's put some values:

y = 2 ^ 1

y = 2

and

y = 2 ^ 2

y = 4

So this is TRUE.

II. The point (1,0) exists in the table.

Let's put 1 into x and see if it gives us 0

y = 2 ^ 1

y = 2

So this is FALSE.

III. As the x-value increase, the y-value decrease.

We have already seen that as x increase, y also increase in part I.

So this is FALSE.

IV. as the x value decrease the y values decrease approaching a singular value.

THe exponential function of this form NEVER goes to 0 and is NEVER negative. So as x decreases, y also decrease and approached a value (that is 0) but never becomes 0.

This is TRUE.

Option I and Option IV are true.