Answer:
Option C. The constant is

Solution:
Let us assume that the constant is c.
Now to the equation will be
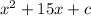 -------- (i)
-------- (i)
We know the square formula
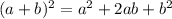
As per the formula we can write the equation as,
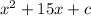
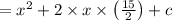
Now if we need make the equation perfect square,
Then as per the formula c should be
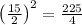
And the equation will be the perfect square as
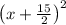
So, the constant is
