Question

A wheel has a radius of 5.9 m. How far (path length) does a point on the circumference travel if the wheel is rotated through angles of (a) 30∘, (b) 30 rad, and (c) 30 rev, respectively? (a) Wheel rotates 30∘. 3.09 m ( ± 0.2 m) (b) Wheel rotates 30 rad. 18.226 m ( ± 20 m) (c) Wheel rotates 30 rev. 1112.1 m ( ± 20 m)

Answer 1

(a). The path length is 3.09 m at 30°.

(b). The path length is 188.4 m at 30 rad.

(c). The path length is 1111.5 m at 30 rev.

Step-by-step explanation:

Given that,

Radius = 5.9 m

(a). Angle
`\theta=30°`

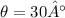
We need to calculate the angle in radian

`\theta=30*(\pi)/(180)`

`\theta=0.523\ rad`

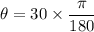
We need to calculate the path length

Using formula of path length

`Path\ length =angle* radius`

`Path\ length=0.523*5.9`

`Path\ length =3.09\ m`

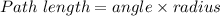
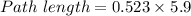
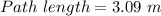
(b). Angle = 30 rad

We need to calculate the path length

`Path\ length=30*5.9`

`Path\ length=177\ m`

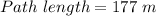
(c). Angle = 30 rev

We need to calculate the angle in rad

`\theta=30*2\pi`

`\theta=188.4\ rad`

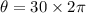
We need to calculate the path length

`Path\ length=188.4*5.9`

`Path\ length =1111.56\ m`

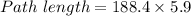
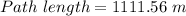
Hence, (a). The path length is 3.09 m at 30°.

(b). The path length is 188.4 m at 30 rad.

(c). The path length is 1111.5 m at 30 rev.