Question

A crate on a motorized cart starts from rest and moves with a constant eastward acceleration ofa= 2.60 m/s^2. A worker assists the cart by pushing on the crate with a force that is eastward andhas magnitude that depends on time. According to F(t) = (5.40 N/s)t. What is the instantaneouspower supplied by this force at t= 4.70 s

Answer 1

To obtain the power, we first need to find the work made by the force.

1) To calculate the work, we need the next equation:

`\int\limits {F} \, dx`

So the force is given by the problem so our mission is to find 'dx' in terms of 't'

2) we know that:

`(dV)/(dt) = a = 2.6`

So we have:

`v = 2.6t`

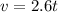
Then:

`(dx)/(dt) = V = 2.6t\\ \\dx = 2.6t*dt`

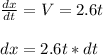
3) Finally, we replace everything:

`\int\limits^(4.7)_(0) {5.4t*2.6t} \, dt`

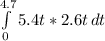
After some calculation, we have as a result that the work is:

161.9638 J.

4) To calculate the power we need the next equation:

`P = (W)/(t)`

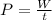
So

P = 161.9638/4.7 = 34.46 W