Answer: C. 0.80920
Explanation:
Given : The average low temperature in the park for May follows a normal distribution with a mean of
 and a standard deviation of
and a standard deviation of
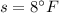 .
.
Let x represents the temperature in the park for May .
Using formula :

For x= 25

Then by using the standard z-table for right tail test,

Hence, the probability that this bag will be warm enough on a randomly selected May night at the park= 0.80920