Question

A particular balloon can be stretched to a maximum surface area of 1257 cm2. The balloon is filled with 3.1 L of helium gas at a pressure of 754 torr and a temperature of 294 K . The balloon is then allowed to rise in the atmosphere. Assume an atmospheric temperature of 273 K and determine at what pressure the balloon will burst. (Assume the balloon to be in the shape of a sphere.)

Answer 1

P = 0.6815 atm

Step-by-step explanation:

Pressure = 754 torr

The conversion of P(torr) to P(atm) is shown below:

`P(torr)=\frac {1}{760}* P(atm)`

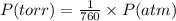
So,

Pressure = 754 / 760 atm = 0.9921 atm

Temperature = 294 K

Volume = 3.1 L

Using ideal gas equation as:

PV=nRT

where,

P is the pressure

V is the volume

n is the number of moles

T is the temperature

R is Gas constant having value = 0.0821 L.atm/K.mol

Applying the equation as:

0.9921 atm × 3.1 L = n × 0.0821 L.atm/K.mol × 294 K

⇒n of helium gas= 0.1274 moles

Surface are = 1257 cm²

For a sphere, Surface area = 4 × π × r² = 1257 cm²

r² = 1257 / 4 × π ≅ 100 cm²

r = 10 cm

The volume of the sphere is :

`V=\frac {4}{3}* \pi* r^3`

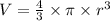
Where, V is the volume

r is the radius

`V=\frac {4}{3}* \frac {22}{7}* {10}^3`

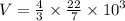
V = 4190.4762 cm³

1 cm³ = 0.001 L

So, V (max) = 4.19 L

T = 273 K

n = 0.1274 moles

Using ideal gas equation as:

PV=nRT

Applying the equation as:

P × 4.19 L = 0.1274 × 0.0821 L.atm/K.mol × 273 K

P = 0.6815 atm