Question

Suppose that a school has 20 classes: 16 with 25 students in each, three with 100 students in each, and one with 300 students, for a total of 1000 students. (a) What is the average class size? (b) Select a student randomly out of the 1000 students. Let the random variable X equal the size of the class to which this student belongs, and define the pmf of X. (c) Find E(X), the expected value of X. Does this answer surprise you?

Answer 1

a) y | p(y)

25 | 0.8

100 | 0.15

300 | 0.05

E(y) = ∑ y . p(y)

E(y) = 25 × 0.8 + 100 × 0.15 + 300 × 0.05

E(y) = 50

average class size equal to E(y) = 50

b) y | p(y)

25 |
`(16* 25)/(1000)=0.4`

100 |
`(3* 100)/(1000)=0.3`

300 |
`(1* 300)/(1000)=0.3`

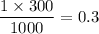
E(y) = ∑ y . p(y)

E(y) = 25 × 0.4 + 100 × 0.3 + 300 × 0.3

E(y) = 130

average class size equal to E(y) = 130

c) Average Student in the class in a school = 50

Average student at the school has student = 130