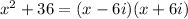Answer:
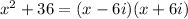
Explanation:
The given expression is
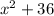
It's understood that this expression is equal to zero
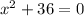
Now, we isolate the variable and then apply a squared root to each side of the equation
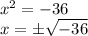
At this point, you'll find that the equation doesn't have solution in the real numbers, that is, all solutions are in the complex numbers. We need to add the imaginary number
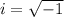 to continue
to continue
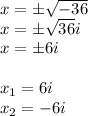
Now, representing these solution as factors, we would have
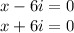
Finally,