Question

A major Blu-ray rental chain is considering opening a new store in an area that currently does not have any such stores. The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with Blu-ray players. It conducts a telephone poll of 300 randomly selected households in the area and finds that 96 have Blu-ray players. The decision on the hypothesis test using a 5% level of significance is

(A) 2.80.
(B) 2.60.
(C) 1.30.
(D) 1.94.

Answer 1

Answer with explanation:

Let p be the population proportion.

Given : The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with Blu-ray players.

i.e.
`p=(5000)/(20000)=0.25`

`H_0:p\leq0.25\\\\H_a:p>0.25`

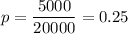
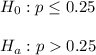
Since alternative hypothesis is right-tailed , so the test is right-tailed test.

Also, Sample size : n= 300 ,

Sample proportion:
`\hat{p}=(96)/(300)=0.32`

Test statistic:
`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

`z=\frac{0.32-0.25}{\sqrt{(0.25(1-0.25))/(300)}}=2.8`

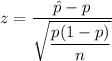
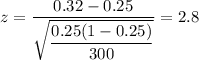
i.e. Observed test statistic Value = 2.80

(A) is right option.

Critical value for 5% significance level for right tailed test :-

`z_(\alpha)=z_(0.05)= 1.6448536`

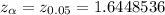
Since , the observed z-value is greater than the critical value , so we reject the null hypothesis.

Conclusion : We have sufficient evidence to supposrt the alternative hypothesis.

So, The chain will open if there is evidence that more than 5,000 of the 20,000 households in the area are equipped with Blu-ray players.