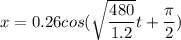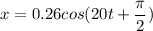Answer:
Step-by-step explanation:
given,
mass of block = 1.2 kg
spring constant (k) = 480 N/m
a) Frequency
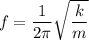
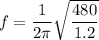
f = 3.183 Hz
b) The position function
x = A cos (ωt + ∅)
at t = 0 , x = 0
0 = A cos ∅
cos ∅ = 0
∅ = π/2
velocity at t= 0 s
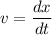
v = Aωsin (ωt + ∅)
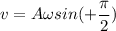
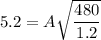
A = 0.26 m
c)