Question

A model rocket is launched straight upward with an initial speed of 56.5 m/s. It accelerates with a constant upward acceleration of 1.96 m/s 2 until its engines stop at an altitude of 198.8 m. What is the maximum height reached by the rocket? Answer in units of m.

Answer 1

Maximum height reached by the rocket, h = 202.62 meters

Step-by-step explanation:

It is given that,

Initial speed of the model rocket, u = 56.5 m/s

Constant upward acceleration,
`a=1.96\ m/s^2`

Distance traveled by the engine until it stops, d = 198.8 m

Let v is the speed of the rocket when the engine stops. It can be calculated using the third equation of motion as :

`v=√(u^2+2ad)`

`v=√((56.5)^2+2* 1.96* 198.8)`

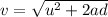
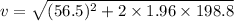
v = 63.02 m/s

At the maximum height, v = 0 and the engine now decelerate under the action of gravity, a = -g. Let h is the maximum height reached by the rocket.

Again using third equation of motion as :

`v^2-u^2=-2gh`

`h=(v^2-u^2)/(-2g)`

`h=(u^2)/(2g)`

`h=((63.02)^2)/(2* 9.8)`

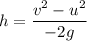
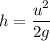
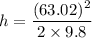
h = 202.62 meters

So, the maximum height reached by the rocket is 202.62 meters. Hence, this is the required solution.