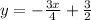Question

Find the equation of a line which passes through the points (-2,3) and (2,0)

Answer 1

y1 - y2 / x1 - x2

3 - 0 / -2 - 2

3/-4

y = mx + b

0 = -3/4(2) + b

0 = -6/4 + b

6/4 = b

y = -3/4x + 6/4

Hope this helps! ;)

Answer 2

The equation of a line which passes through the points (-2,3) and (2,0) is
`3 x+4 y=6 \text { or } y=-(3 x)/(4)+(3)/(2)`

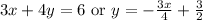
Solution:

Let us assume that the
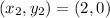`(x_2, y_2) = (2,0)` and
`(x_1, y_1) = (-2,3)`

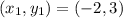
The slope of the line m is
`=(y_2-y_1)/(x_2-x_1)=(0-3)/(2-(-2))=\left(-(3)/(4)\right)`

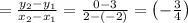
We know the equation of a line at a given point
`(x_1, y_1)` is
`(y-y_1) = m(x-x_1)`

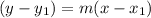
Let me take the point (2,0) here,

So the equation of the line is

`\Rightarrow(y-0)=\left(-(3)/(4)\right)(x-2)`

`\Rightarrow y=\left(-(3)/(4)\right)(x-2)`

`\Rightarrow 4 y=(-3) *(x-2)`

`\Rightarrow 4 y=-3 x+6`

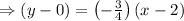
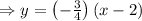
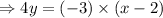
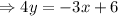
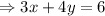`\Rightarrow 3 x+4 y=6 \text` or
`y=-(3 x)/(4)+(3)/(2)`

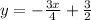
So, the equation is
`3 x+4 y=6`

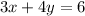
Or
`y=-(3 x)/(4)+(3)/(2)`