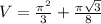Question

The region R is bounded by y = sin x and the x-axis on the interval [0, 2π/3]. Write a definite integral for the volume V of the solid formed when R is revolved around the x-axis and then find V. Type pi for π if needed in the integral limits.

Answer 1

The integral is

`\displaystyle\pi\int_0^(2\pi/3)\sin^2x\,\mathrm dx`

Recall the double angle identity,

`\sin^2x=\frac{1-\cos(2x)}2`

Then the volume is

`\displaystyle\frac\pi2\int_0^(2\pi/3)(1-\cos(2x))\,\mathrm dx=\frac\pi2\left(x-\frac12\sin(2x)\right)\bigg|_0^(2\pi/3)`

`=\displaystyle\frac\pi2(\frac{2\pi}3-\frac12\sin\frac{4\pi}3\right)`

`=\boxed{\frac{\pi^2}3+\frac{\pi\sqrt3}8}`

Answer 2

`V=(\pi^2)/(3)+(\pi\sqrt3)/(8)`

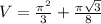
Explanation:

We are given that a region R is bounded by y= sin x and x- axis on the interval
`[0,(2\pi)/(3)]`

We have to write definite integral for the volume V of solid formed by R is revolved about x- axis and we have to find V.

Volume of solid is given by

`V=\pi \int_(0)^{(2\pi)/(3)} sin^2 xdx`

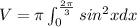
We know that
`sin^2x=(1-cos2x)/(2)`

`V=(\pi)/(2) \int_(0)^{(2\pi)/(3)} (1-cos 2x) dx`

`V=(\pi)/(2)(x-(sin2x)/(2))^{(2\pi)/(3)}_(0)`

`V=(\pi)/(2)((2\pi)/(3)-(1)/(2)sin(4\pi)/(3))`

`V=(\pi)/(2)((2\pi)/(3)-(1)/(2)sin(\pi+(\pi)/(3)))`

`V=(\pi)/(2)((2\pi)/(3)+(1)/(2)sin(\pi)/(3))`

`sin(\pi+(\pi)/(3))=-sin(\pi)/(3)=-(\sqrt3)/(2)`

`V=(\pi)/(2)((2\pi)/(3)+(1)/(2)\cdot(\sqrt3)/(2))`

`V=(\pi^2)/(3)+(\pi\sqrt3)/(8)`

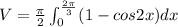
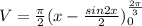
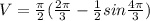
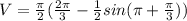
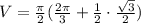
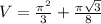
Hence, the volume of solid when R is revolved around the x- axis=
`V=(\pi^2)/(3)+(\pi\sqrt3)/(8)`