Question

An object is thrown vertically upward such that it has a speed of 75 m/s when it reaches two thirds of its maximum height above the launch point. Determine the maximum height h. The acceleration of gravity is 9.8 m/s² .

(a)96m
(b)32m
(c)48 m
(d)75m
(e)64m

Answer 1

The maximum height is equal to 860.04m

Why?

We can find the maximum height of the object in two steps.

First step: Finding the initial speed.

`v_(f)^(2)=v_(o)^(2)-2*g*d\\\\0=v_(o)^(2)-2*(9.81(m)/(s^(2)))*hmax\\\\hmax=(v_(o)^(2))/(2*9.81(m)/(s^(2) ))`

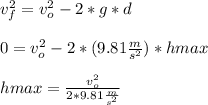
Then,

`v_(f)^(2)=v_(o)^(2)-2*g*d\\\\(75(m)/(s))^(2) =v_(o)^(2)-2*(9.81(m)/(s^(2)))*(2)/(3)(v_(o)^(2))/(2*9.81(m)/(s^(2) ))\\\\5625(m^(2) )/(s^(2))=v_(o)^(2)-(2)/(3)v_(o)^(2)\\\\3*5625(m^(2) )/(s^(2))=v_(o)^(2)\\\\v_(o)=\sqrt{3*5625(m^(2) )/(s^(2))}=129.90(m)/(s)`

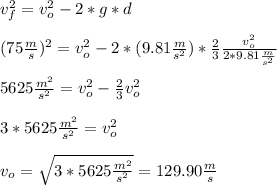
Second step: Find the maximum height.

Now, again using the second equation, we need to subsitutite the obtained value for the initial speed into it, so:

`hmax=((129.90(m)/(s))^(2))/(2*9.81(m)/(s^(2) ))=860.04m`

Hence, we have that the maximum height is equal to 860.04 meters.

Have a nice day!