Question

You are standing at the top of a cliff that has a stairstep configuration. There is a vertical drop of 6 m at your feet, then a horizontal shelf of 5 m , then another drop of 4 m to the bottom of the canyon, which has a horizontal floor. You kick a 0.97 kg rock, giving it an initial horizontal velocity that barely clears the shelf below. 5 m ∆x 10 m v 6 m 4 m What initial horizontal velocity v will be required to barely clear the edge of the shelf below you? The acceleration of gravity is 9.8 m/s 2 . Consider air friction to be negligible. Answer in units of m/s.\

Answer 1

4.5 m/s

Step-by-step explanation:

The rock must barely clear the shelf below, this means that the horizontal distance covered must be

`d_x = 5 m`

while the vertical distance covered must be

`d_y = 6 m`

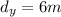
The rock is thrown horizontally with velocity
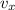`v_x`, so we can rewrite the horizontal distance as

`d_x = v_x t`

where t is the time of flight. Re-arranging the equation,

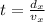`t=(d_x)/(v_x)` (1)

The vertical distance covered instead is

`d_y = (1)/(2)gt^2`

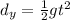
where we omit the term
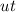`ut` since the initial vertical velocity is zero. From this equation,

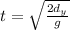`t=\sqrt{(2d_y)/(g)}` (2)

Equating (1) and (2), we can solve the equation to find
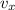`v_x`:

`(d_x)/(v_x)=\sqrt{(2d_y)/(g)}\\(d_x^2)/(v_x^2)=(2d_y)/(g)\\v_x = d_x \sqrt{(g)/(2d_y)}=5\sqrt{(9.8)/(2(6))}=4.5 m/s`